こんにちは。PlayGroundのデータコースに所属しているTaichi(Ando)です。今回不動産の価格推定プロジェクトにてブラックボックスモデルの振る舞いを解釈する手法であるSHAPを扱ったので皆さんにも紹介していきたいと思います。(この記事は実装編ですので理論的な部分については理論編をご覧ください。)
SHAPとは
SHAPは、協力ゲーム理論の概念であるシャープレイ値に着想を得て開発されたライブラリで、あらゆる機械学習モデルにおける局所的な特徴量の目的変数への寄与度(貢献度)を計算、可視化することができるものです。早速その実装方法を見ていきましょう。
想定するタスク
今回は、ボストンにおける住宅価格を予測する機械学習モデルを作る中で、各住宅地それぞれの特徴量の住宅価格に対する影響や寄与度(貢献度)を知りたいというケースを想定していきます。まずは回帰タスクで広く使われているモデルであるlightGBMで予測モデルを作っていきましょう。また、データセットに関してはThe Boston Housing Datasetを使用していきます。(*この記事内では「寄与度、貢献度、影響」という言葉が出てきますがどれも同じ意味です。)
Let's 実装
まずは今回使用するライブラリをimportしていきます。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
import lightgbm as lgb
import shap
import pandas as pd
import numpy as npデータセットをロードしてデータの中身を見てみます。
boston_data = load_boston()
df = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
df.head()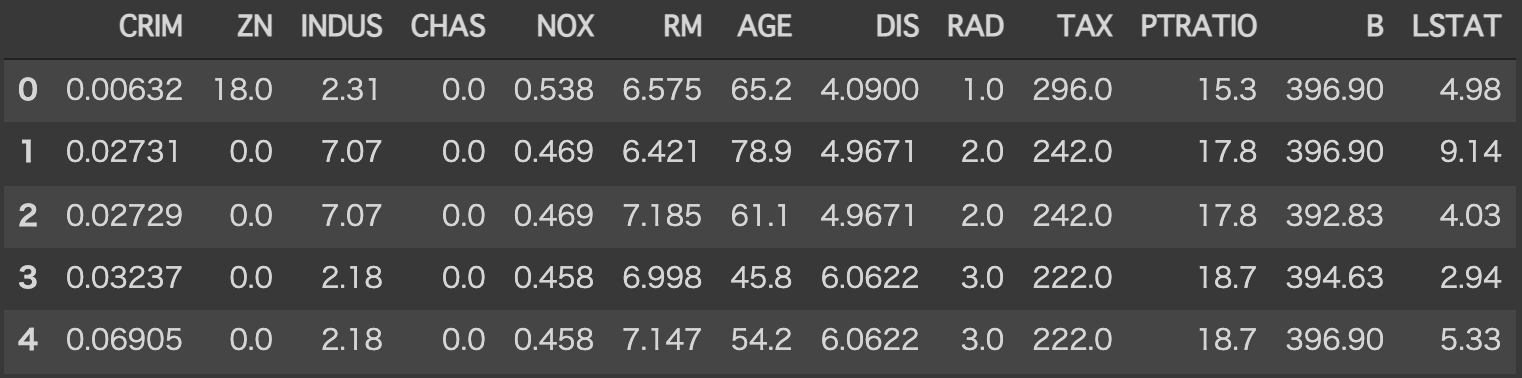
各特徴量の構成は以下のようになっています。(参考サイト)また今回の目的変数は506個の地域における持家住宅の1000ドル単位の価格中央値です。
| CRIM | 人口 1 人当たりの犯罪発生数 |
|---|---|
| ZN | 25,000 平方フィート以上の住居区画の占める割合 |
| INDUS | 小売業以外の商業が占める面積の割合 |
| CHAS | チャールズ川によるダミー変数 (1: 川の周辺, 0: それ以外) |
| NOX | NOx の濃度 |
| RM | 住居の平均部屋数 |
| AGE | 1940 年より前に建てられた物件の割合 |
| DIS | 5 つのボストン市の雇用施設からの距離 (重み付け済) |
| RAD | 環状高速道路へのアクセスしやすさ |
| TAX | $10,000 ドルあたりの不動産税率の総計 |
| PTRATIO | 町毎の児童と教師の比率 |
| B | 町毎の黒人 (Bk) の比率を次の式で表したもの。 1000(Bk – 0.63)^2 |
| LSTAT | 給与の低い職業に従事する人口の割合 (%) |
この記事はSHAPの実装方法についてわかりやすく見ていくものですので、今回は特に特徴量エンジニアリングなどはせずにモデルを作成していきます。
データをtrainデータとtestデータに分割します。
X = df
y = boston_data.target
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size=0.2, shuffle=True, random_state=2022)分割したデータを用いてモデルを作成し、学習させていきます。
lgb_train = lgb.Dataset(train_X, train_y)
lgb_test = lgb.Dataset(test_X, test_y, reference=lgb_train)
params = {
'task': 'train',
'boosting_type': 'gbdt',
'objective': 'regression',
'metric': {'rmse'},
'learning_rate': 0.05,
'num_leaves': 21,
'min_data_in_leaf': 2,
'num_iteration': 1500,
'verbose': 0
}
model = lgb.train(params,
train_set=lgb_train,
valid_sets=lgb_test,
early_stopping_rounds=1000)モデルが作成できたら、SHAPを用いて寄与度を計算してみましょう。今回寄与度を見ていくデータはモデルに学習させたデータとします。
explainer = shap.Explainer(model)
shap_values = explainer(X)1番最初のデータに関しての寄与度(SHAP値)を見てみましょう。
np.set_printoptions(suppress=True) #指数表現の禁止
shap_v = pd.DataFrame(shap_values.values[0].reshape(1, -1), columns=boston_data.feature_names)
shap_v
SHAPには 寄与度を可視化する機能も幾つか備わっています。実際に使いながら紹介していきます。1番目のデータの寄与度について可視化して見ていきます。
Waterfall Plot
特徴量を寄与度順にグラフにしてくれます。
shap.plots.waterfall(shap_values[0])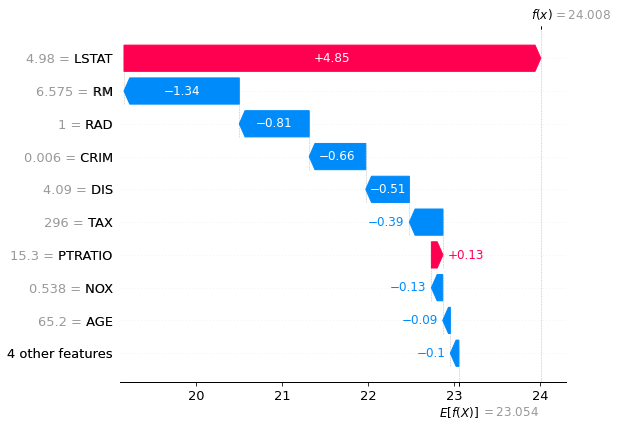
目的変数に正の寄与度を持つ特徴量のグラフは赤色に、負の寄与度を持つ特徴量のグラフは青色に色分けされています。また上の図のE[f(X)]=23.054は全データの目的変数の平均値を表します。目的変数の単位が1000ドルであることに注意しながらこのグラフを解釈すると「1番目のデータはLSTAT(給与の低い職業に従事する人口の割合)が住宅価格に4850ドルプラスの影響があり、RM(住居の平均部屋数)が1340ドルマイナスの影響があり‥‥」というふうに各特徴量の目的変数への影響具合がわかり、結果として予測値が24.008(24008ドル)になったということが読み取れます。このようにして各データの各特徴量の目的変数への影響具合がわかるようになるのです。
Force Plot
正の影響を持つ特徴量と負の影響を持つ特徴量を分けて数直線上にプロットしてくれます。
shap.initjs()
shap.plots.force(shap_values[0])
また、上のグラフを90度回転し全体のグラフとして全データまとめてプロットすることもできます。
shap.initjs()
shap.plots.force(shap_values)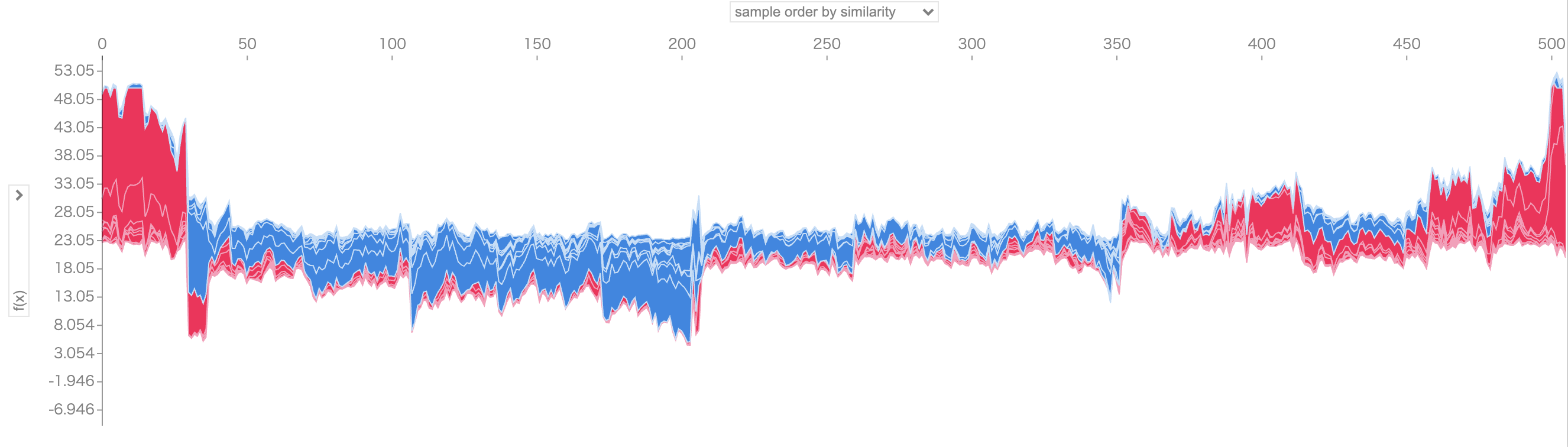
Scatter Plot
全体のデータより、1つの特徴量がモデルにどのような影響を与えるかについて横軸に特徴量の値、縦軸にその特徴量のSHAP値(寄与度)をプロットすることができます。試しにRM(住居の平均部屋数)という特徴量についてScatter Plotを描いてみましょう。
shap.plots.scatter(shap_values[:,"RM"])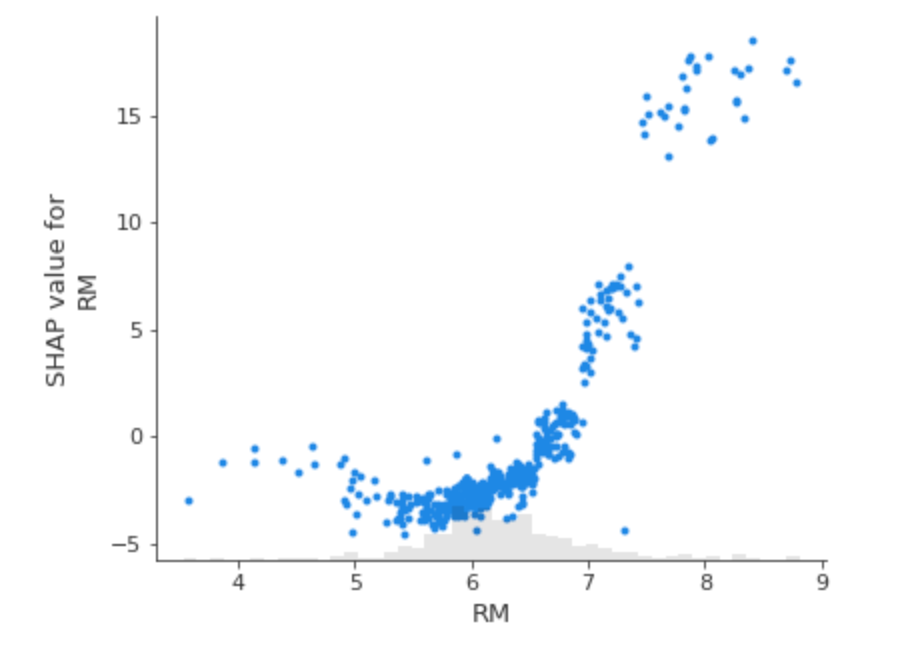
上の図から、「住居の平均部屋数が増えれば増えるほど、SHAP値が大きくなる」ということが読み取れます。つまり、「住居の平均部屋数が増えれば増えるほど、住宅価格への影響は正の方向に大きくなっていく(住宅価格は高くなる傾向にある)」ということが解釈できるわけです。
Beeswarm Plot
どの特徴量がモデルに対して重要であるのかを知るのに、全ての特徴量のSHAP値をプロットできるBeeswarm Plotがあります。以下のプロットは、全データのSHAP値の大きさの合計で特徴をソートし、SHAP値を使って各特徴がモデル出力に与える影響の分布を描いてくれます。
shap.plots.beeswarm(shap_values)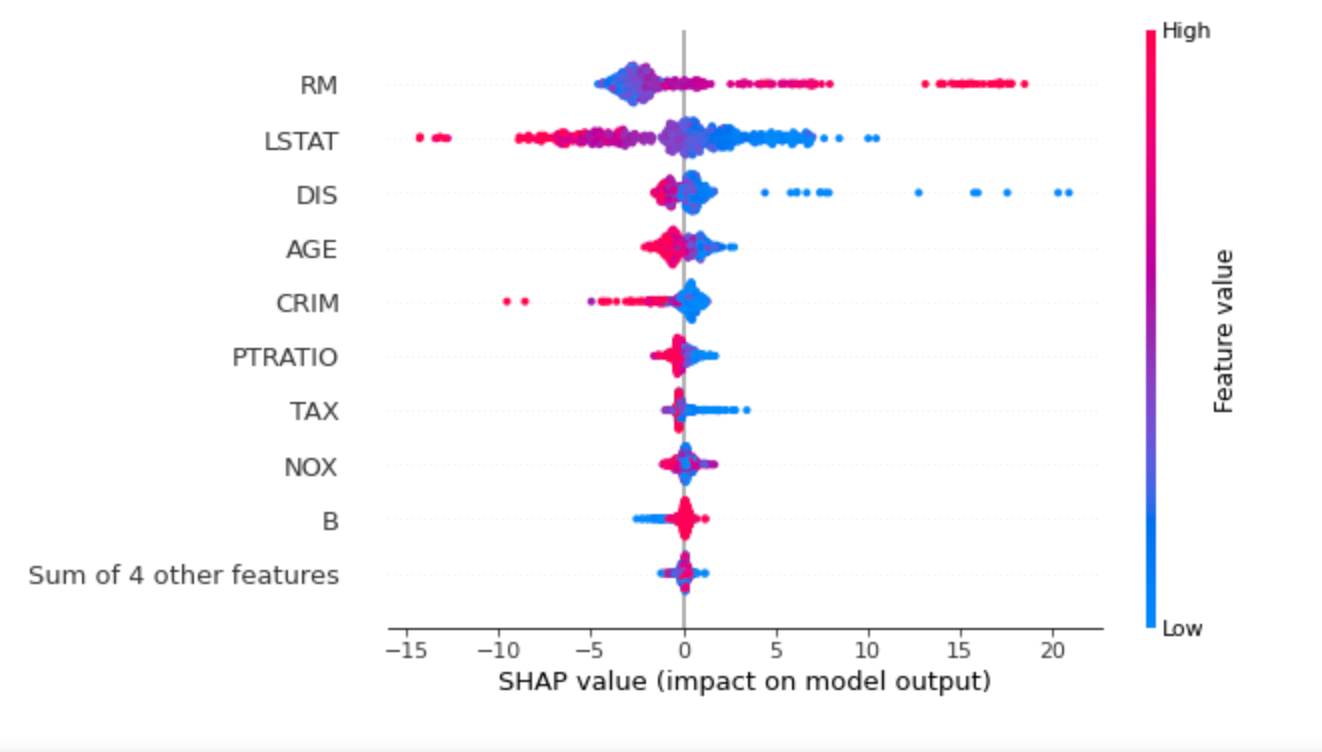
まとめ
ここまでSHAPの使い方を見てきました。SHAPにより機械学習モデルの解釈性が上がることがご理解いただけたと思います。是非1度使ってみてはいかがでしょうか。ありがとうございました。
参考文献
SHAP documentation: https://shap.readthedocs.io/en/latest/index.html
![[Solidity]実例から学ぶ、ガス最適化のTips](/content/images/2022/01/----------2022-01-11-0.41.08.png)