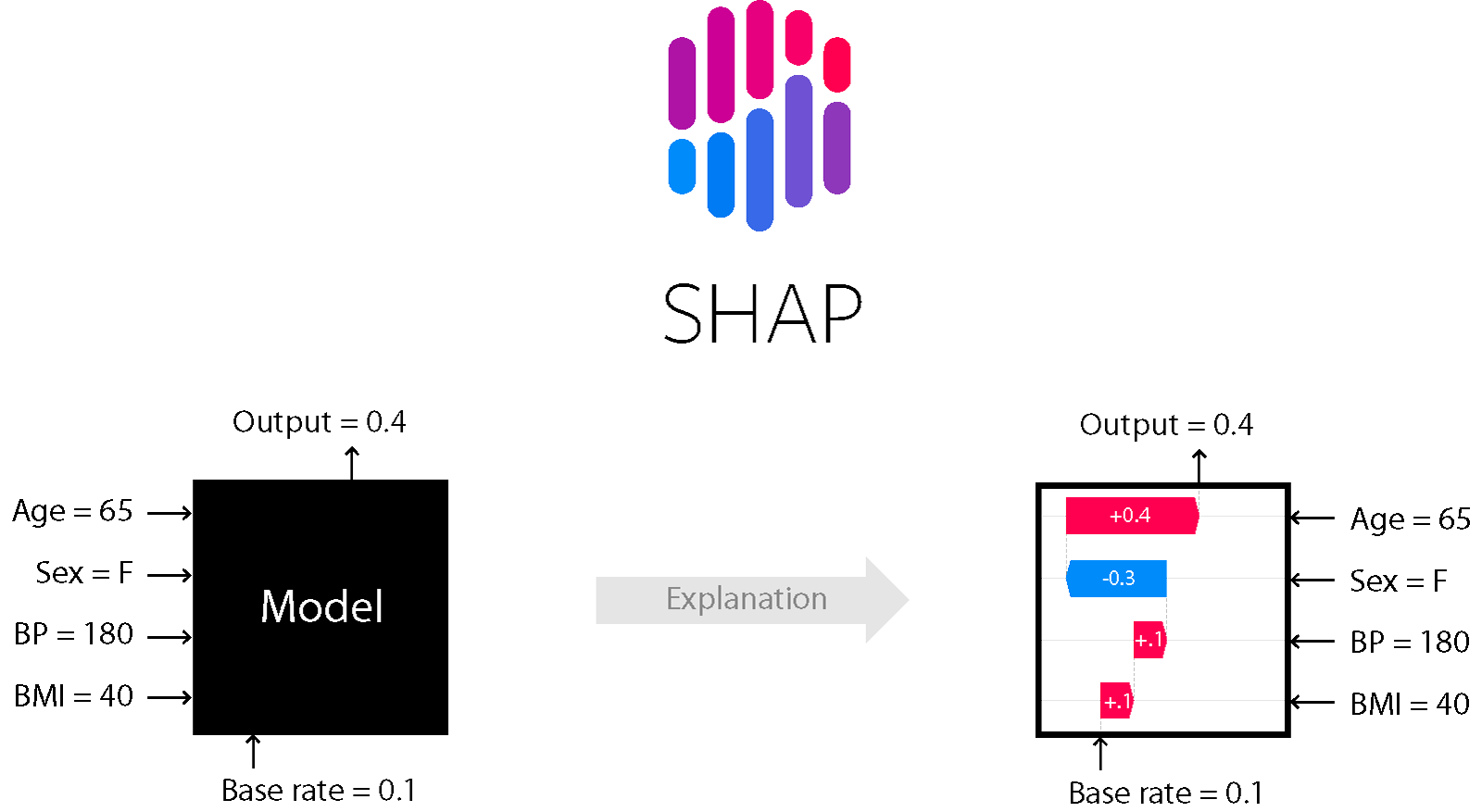
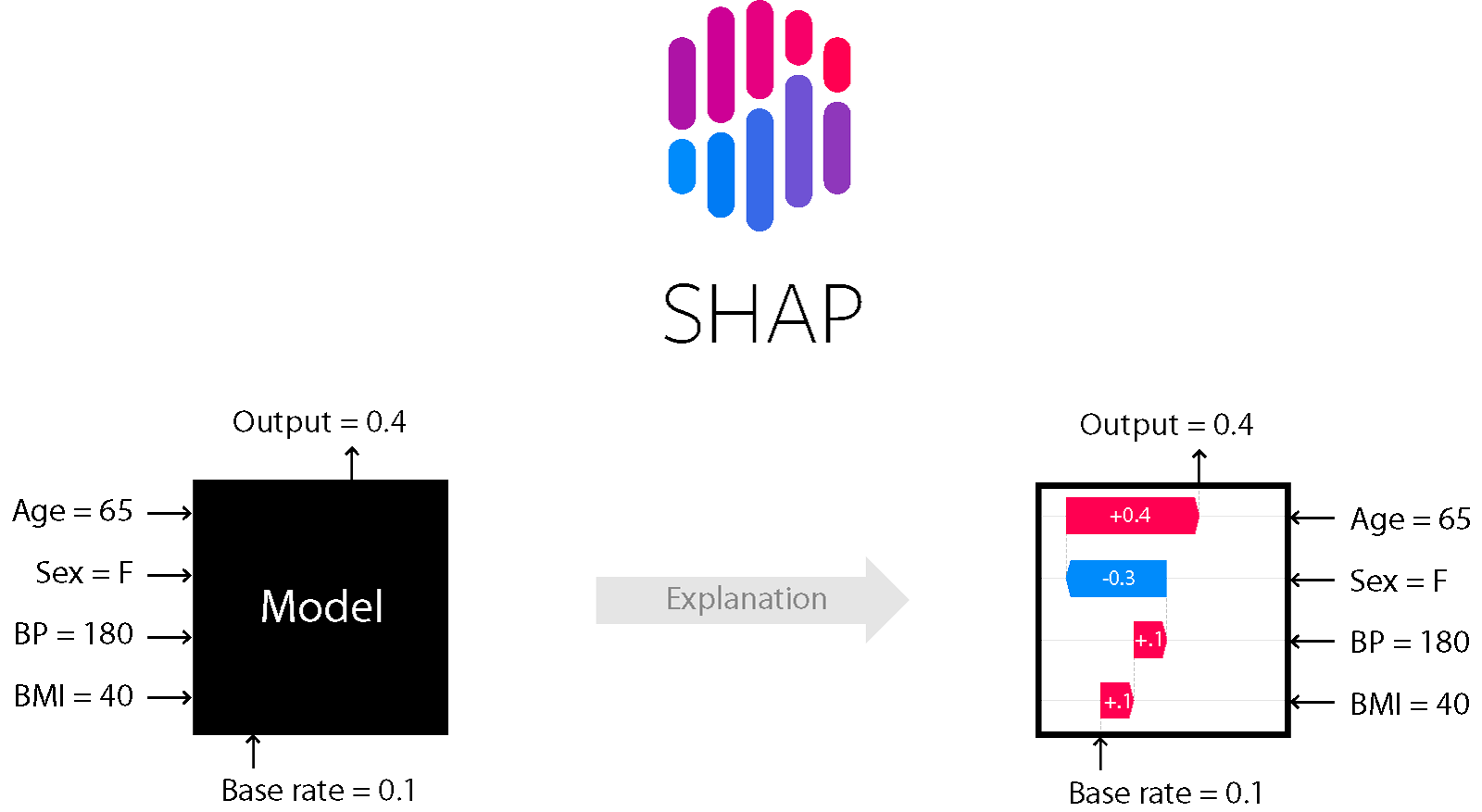
こんにちは。PlayGroundのデータコースに所属しているTaichi(Ando)です。今回不動産の価格推定プロジェクトにてブラックボックスモデルの振る舞いを解釈する手法であるSHAPを扱ったので皆さんにも紹介していきたいと思います。（この記事は理論編ですので具体的な実装方法については実装編をご覧ください。）

ブラックボックスモデルとは

そもそもブラックボックスモデルとはなんでしょうか。日々世界中で機械学習の研究と開発が進み、データサイエンスを初めたばかりの初心者でも高い精度の予測モデルを容易に構築できます。ディープラーニング、勾配ブースティング決定木(GBDT)などのモデルは高精度の予測を可能とし、それらが実装されたオープンソースのパッケージも充実しています。しかし、高性能が故にその機械学習モデルの仕組みは複雑で、線形回帰のように一目でその振る舞いを理解する（解釈する）ことは困難です。このように、データを学習させ予測させて出た結果に対して、なぜそのような予測が出力されたのか、どのような仕組みで計算がされているのかを理解することが難しい機械学習モデルをブラックボックスモデルと言います。

現場で求められるもの

データ分析やAI作成プロジェクトの現場では、まず第一にモデルの精度が求められます。実務における予測精度はユーザーの利潤に直結する重要な要素であり、モデルに大きな誤差が存在することはユーザーのリスクに繋がるからです。また現場ではただ精度が良ければよいということはほとんどなく、モデルが出力した結果に対して、その理由を示すモデルの解釈性も必要になってきます。モデルがなぜそのように判断を下したのかを理解することができないと、実はそのモデルは実験のときだけ良い精度を出しているだけであったり、人間の考えとはかけ離れた結果を出力するモデルであったりと、データとの整合性がないモデルが作成されている可能性があるからです。

SHAPとは

前置きが長くなりましたがSHAPについて紹介していきたいと思います。SHAPは様々な機械学習モデルの解釈性を与えるPythonのライブラリです。協力ゲーム理論の概念であるシャープレイ値という値からその名前が付けられています。シャープレイ値は一言で言うと貢献度の期待値です。

シャープレイ値とは

貢献度の期待値だけだとよくわからないと思うので例を挙げて考えていきたいと思います。

今、Aさん,Bさん,Cさんが報酬がもらえるゲームに参加するとします。Aさんが一人で参加すると6万円ゲット、Bさんと協力して二人で参加すると20万円ゲット…と言うように一人、二人で参加したり三人で参加した場合の報酬の表が下の表であったとします。

この時、三人でこのゲームに参加したとすると報酬の24万円はどのように分けたら良いでしょうか？公平に分配するのであれば、それぞれのプレイヤーのゲームへの貢献度に従って分けた方がフェアです。ではどうやって各プレイヤーの貢献度を算出するのか。それには限界貢献度という値を使います。ここでの限界貢献度とは「各プレイヤーがゲームに参加した時、しなかった時に比べてどのくらい報酬が増えたか」を表します。

たとえば、Aさん一人でゲームに参加した時とAさんとBさんが協力して二人で参加した時は6万円と20万円ですから14万円の差があります。つまりこの場合のBさんの限界貢献度は14万円ということになります（Aさんだけだと6万円しか獲得できないが、そこにBが参加すると報酬が14万円増えるということです）。もう一つ例をあげると、A,Cの二人で参加していた場合とA,B,Cの三人で参加していた場合は15万円と24万円ですからこの場合のBさんの貢献度は9万円ということになります。このようにして各プレイヤーの限界貢献度をプレイヤー形成の順番（参加順）で表にすると下のようになります。上の例でも分かる通り、限界貢献度は参加順に依存して変わることに注意してください。

ここで各プレイヤーの平均的な限界貢献度を求めると、これがシャープレイ値になります。実際に各プレイヤーのシャープレイ値を求めると、

• Aさんのシャープレイ値=(6+6+16+14+13+14)/6=11.5万円
• Bさんのシャープレイ値=(14+9+4+4+9+8)/6=8万円
• Cさんのシャープレイ値=(4+9+4+6+2+2)/6=4.5

このようにして、シャープレイ値に応じて配分を実行することで、公平な報酬の分配が可能になります。シャープレイ値は「そのプレイヤーが協力することで、平均的にどのくらい報酬が増えるのか」を表す値であるということがわかっていただけたと思います。

さて、次にこれを機械学習に応用することで、どのようにブラックボックスモデルに解釈性を与えるのかを解説していきたいと思います。

シャープレイ値の機械学習への応用

これまでに説明したシャープレイ値についての特性を機械学習に応用していこうと思います。今回は回帰タスクにおけるシャープレイ値の応用を考えていきます。

シャープレイ値は前述の例で「そのプレイヤーが協力することで、平均的にどのくらい報酬が増えるのか」を表す値でしたが、これをプレイヤー＝特徴量、報酬＝目的変数とすると「その特徴量が加わると、平均的にどのくらい目的変数の値が増えるのか」ということを表す値になることがわかると思います。このようにして、特徴量の目的変数への影響が分かるようになり、結果としてモデルの振る舞いが理解できるようになるのです。

例としては、物件価格を予測する回帰モデルを作ったときに、使用している特徴量についてシャープレイ値を計算することで、例えば「駅からの距離」という特徴量についてのシャープレイ値が大きいマイナスの値を取る場合、そのデータでは「駅からの距離」という特徴量は物件価格に対して大きくマイナスの影響を持つことを意味し、特徴量の目的変数に対する影響を解釈することができるわけです。しかし、説明変数の数が大きくなると計算に時間がかかるため、実際にSHAPで行われている計算はシャープレイ値の近似解を求めるように工夫されています。

まとめ

ここまで、シャープレイ値の理論について考えてきました。回帰タスクにおけるシャープレイ値は「その特徴量が加わると、平均的にどのくらい目的変数の値が増減するのか」という値であることがわかっていただけたでしょうか。今回は理論編ということなので実装はしませんでしたが、次回は実際に実装してみながらSHAPというライブラリの使い方や便利さについて触れていきたいと思います。ありがとうございました。

参考文献

SHAP documentaton: https://shap.readthedocs.io/en/latest/index.html

SHAP を用いて機械学習モデルを説明する |Data-Robot: https://www.datarobot.com/jp/blog/explain-machine-learning-models-using-shap/