大学でも PlayGround でも機械学習の勉強をしている yuji です。今回は、統計や機械学習の分野でよく使われる３つの数式

• 平均
• 平均二乗誤差関数（RMSE）
• 正規方程式

を僕はどのようにイメージしているかを紹介します。理解に行き詰まってしまったら理論的な部分は飛ばしつつ図や例えに沿ってぜひ最後まで読んでいただけたら幸いです。

平均

データが手元にあるときは、データの合計を個数で割るという公式が使われます。（標本平均）

$$ \frac{1}{N} \sum_{i=1}^N x_i = \frac{x_1 + x_2 + \cdots x_N}{N} $$

可能かどうかは置いといて、仮に世の中にあるすべてのデータを手に入れたときにそれらの平均を求めたいときは、下式を使います。（期待値）（この解釈があっているのかは分かりません。）

$$ \text{E} [X] = \int x p(x) ~\text{d}x $$

積分を使うことで $x$ が無限通りの値を取る場合も考慮することができます。

さて、ここからが本題です。僕は１年生で履修した物理の授業でこのような公式に出会いました。

$$ G =\int xm(x) ~\text{d}x $$

これは物体の重心の座標を求めるための公式です。（簡単のために、物体全体の質量は１としています。）

参考: https://science-log.com/数学/図形の重心を解析的に求める方法/

記号が違うだけで完全に同じ形ですよね？物理において重心とは重力の釣り合いが取れる点、つまり指一本で支えられる点を意味します。本を指一本で支えるには真ん中に置けばいいですが、金槌のように位置によって密度が異なる物体を支えるには、重い方にずらさなければなりません。

式の形が同じということは、確率分布に対しても同様に解釈しても良いはずです。

このように、僕は「平均」とは分布を下から支えられる位置というイメージを持っています。真ん中でも山になっている位置でもありません。

平均二乗誤差関数（RMSE）

下式で表される平均二乗誤差関数は最もよく使われるな誤差関数です。

$$ \text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^N (y_i - t_i)^2} $$

ここで、$y_i$ は モデルの予測で、$t_i$ は観測値とします。すると、$(y_i - t_i)$ は差なので予測の外れ具合と解釈できます。では、二乗して平均をとってルートを取ることにはどんな意味があるのでしょう。

多くの人が気づいているかもしれませんが、定数倍すればこの式の形はユークリッド距離と一致します。ユークリッド距離とは、点 P と点 Q の距離を P と Q を結んだ線の長さであると定義した最も直感的な距離です。

参考: https://ja.wikipedia.org/wiki/ユークリッド距離#N次元

観測値をヒトの力で変えることはできませんが、モデルのアルゴリズムを変えれば予測値は変えることができます。つまり、誤差を減らすことでモデルを改善することは、固定された点 Q に点 P を動かして近づけることと等価です。

正規方程式

先程の話で点 P を動かして点 Q に近づけるという話が出てきましたが、どこまで近づけられるのでしょうか。それは正規方程式から考えることができます。（一瞬だけ大学数学がでてきます。）

$$ \hat{w} = (X^T X)^{-1} X^T t $$

正規方程式とは、$y = Xw$ で定められたモデルの最適なパラメータ $\hat{w}$ を求めるときに使う公式です。ここで $w$ に $\hat{w}$ を代入すると、

$$ y = X\hat{w} = X(X^T X)^{-1} X^T t = P ~ t \newline (P = X(X^T X)^{-1} X^T) $$

$P$ という射影行列と呼ばれる形が現れます。と言われても、大学でもあまり見かけない式です。

参考: https://manabitimes.jp/math/2486

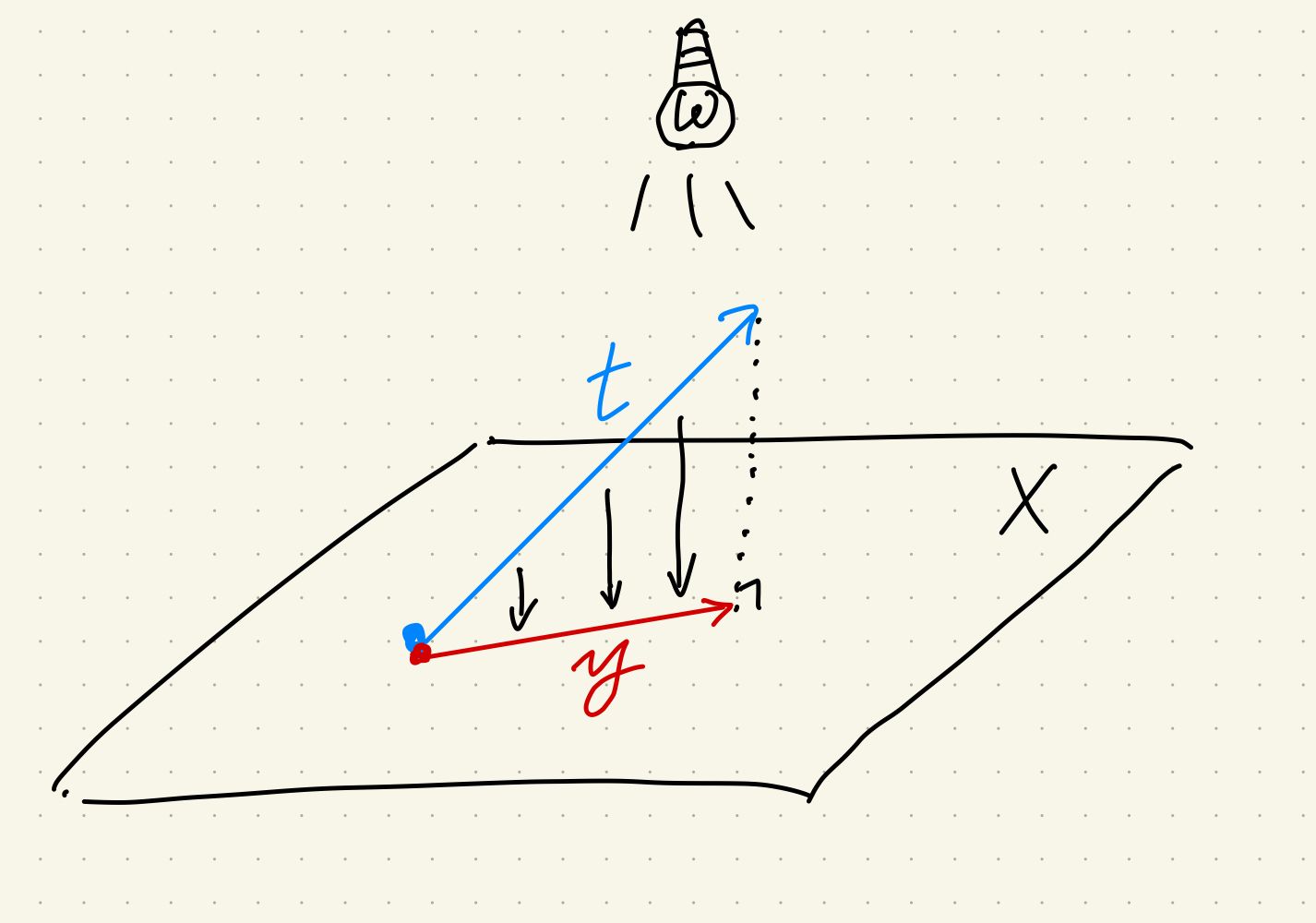
名前の通り射影 $P$ とは、$t$ という矢印を $X$ というスクリーンに写すことを言い、スクリーンに写った影に当たるのが左辺の $y$ です。よく射影に $P$ や $p$ という記号が使われるのは、projection の頭文字から来ています。（写像が mapping だから 射影写像はプロジェクション・マッピングだったりして。）

射影とは、いくつかの次元を消す操作です。例えば、三次元の世界を写真に収めたら奥行きという次元を消した二次元の影ができます。しかし、写真は制限された空間でそれ以上のものを表現しようとしています。

ではなぜ、パラメータ最適化の話に射影がでてくるのでしょうか。それは、モデルも同様に制限された空間からなんとか現実を表現しようとしているからです。例えば、

$$ y = ax^2 + bx + c $$

というモデルは 2 次関数までしか表現できないという制限があります。

より詳しくすると、パラメータの最適化とは、固定された $t$ に限られた領域（下図では $X$ という矢印の上）でしか動けないモデル $y$ を近づけることを指します。その近さを測るが先程の RMSE のような誤差関数です。

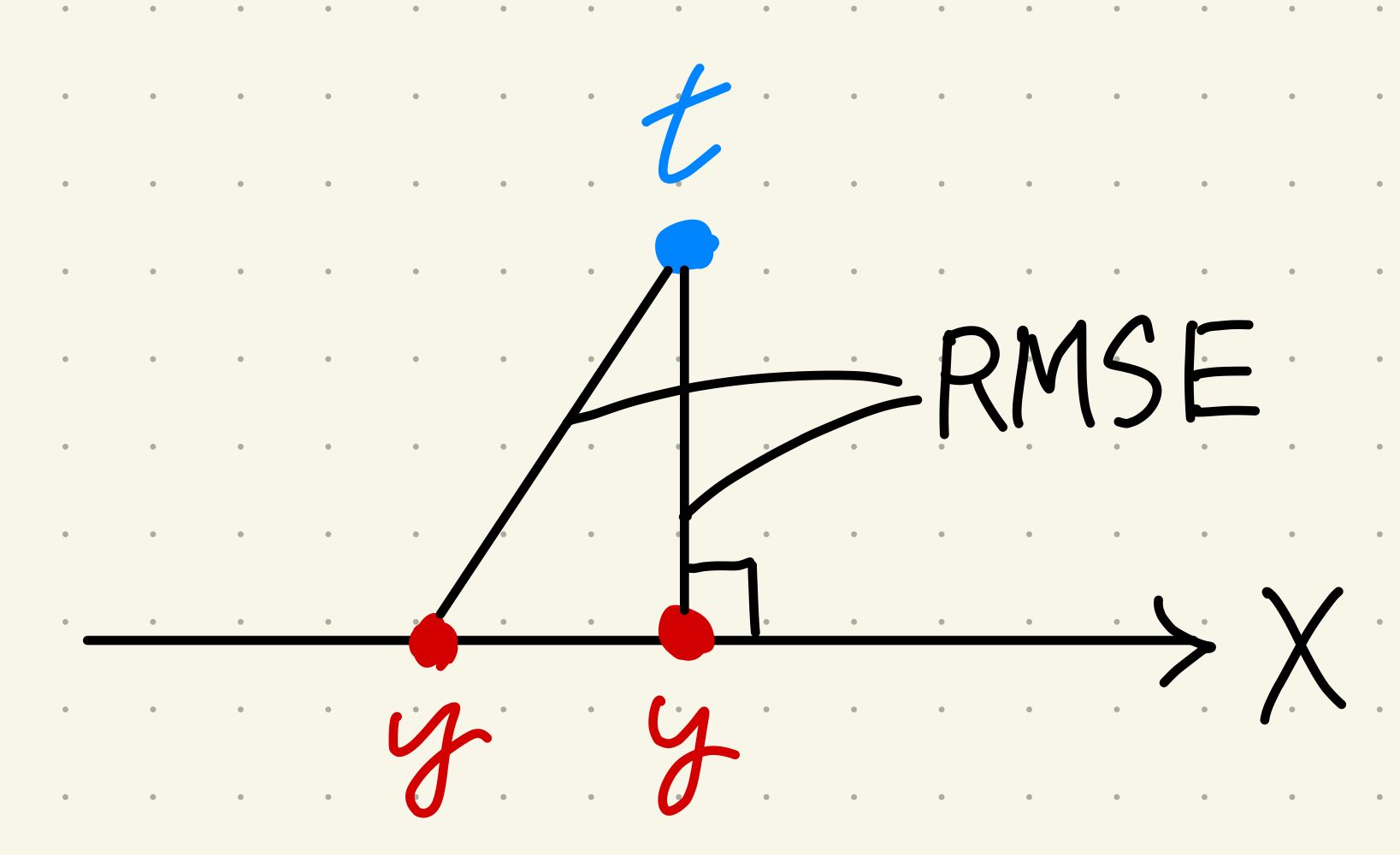
そして、モデル $y$ が $t$ の射影になったとき、つまり影になったときに誤差関数は最小になり、最適なモデルが完成します。

射影をすると次元が減るので情報が失われてしまうのではないかと思われるかもしれません。マスコットの写真を取るとき、奥行きが失われるので一番カメラに近い表面部分しか写真に残すことができません。別に、中身のオジ○ンを撮りたい訳ではないのでそれで十分なのです。

とても冗長な現実世界のデータからいらない情報を削ぎ落として欲しい情報だけを取り出すことが機械学習の目的なのです。

正射影についての補足

行列 $X$ をベクトル $x$ に書き直して -1 乗を分数にしたら、高校の教科書にも載っている正射影の公式になります。

$$ y = \frac{x^T t}{x^T x}x $$